Пи (число)

В искусстве и маркетинге

Несмотря на то, что Пи – это математическая константа, на протяжении многих лет люди пытались использовать иррациональное и загадочное значение и в других сферах жизни, в том числе в произведениях искусства.

Самые первые признаки постоянной были найдены в памятнике архитектуры в Гизе. При определении размеров Великой пирамиды выяснилось, что отношение периметра её основания к высоте равно π. Неизвестно только, хотел ли использовать архитектор свои знания об этом числе, или такое соотношение вышло случайно.

В настоящее время число Пи также не обделено вниманием в творчестве. К примеру, если обозначить каждую ноту минорной гаммы цифрой от 0 до 9, а затем наиграть полученную последовательность в виде числа Пи на музыкальном инструменте, можно насладиться необычной мелодией с интересным звучанием

Постоянная также не обошла стороной кинематограф. Драматический фильм под названием «Пи: вера в хаос» получил награду за лучшую режиссуру на фестивале кино Санденс. По сюжету главный герой находится в поисках простых и понятных ответах на вопросы о константе, что в результате почти довело его до сумасшествия. Упоминания числа встречаются также в других кинофильмах и сериалах.

Своё применение число нашло даже в такой неожиданной области, как маркетинг. Так, компанией Гивенчи был выпущен одеколон под названием «Пи».

Мнемонические правила

Чтобы нам не ошибаться,
Надо правильно прочесть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Надо только постараться
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Три, четырнадцать, пятнадцать,
Девять, два, шесть, пять, три, пять.
Чтоб наукой заниматься,
Это каждый должен знать.
Можно просто постараться
И почаще повторять:
«Три, четырнадцать, пятнадцать,
Девять, двадцать шесть и пять.»

2.
Подсчитайте количество букв в каждом слове в нижеприведенных фразах (без учета знаков препинания
) и запишите эти цифры подряд — не забывая про десятичную запятую после первой цифры «3», разумеется. Получится приближенное число Пи.

Это я знаю и помню прекрасно: Пи многие знаки мне лишни, напрасны.

Кто и шутя, и скоро пожелаетъ Пи узнать число — ужъ знаетъ!

Вот и Миша и Анюта прибежали Пи узнать число они желали.

(Вторая мнемоническая запись верна (с округлением последнего разряда) только
при использовании дореформенной орфографии : при подсчете количества букв в словах необходимо учитывать твердые знаки!)

Еще один вариант этой мнемонической записи:

Это я знаю и помню прекрасно:
Пи многие знаки мне лишни, напрасны.
Доверимся знаньям громадным
Тех, пи кто сосчитал, цифр армаду.

Раз у Коли и Арины
Распороли мы перины.
Белый пух летал, кружился,
Куражился, замирал,
Ублажился,
Нам же дал
Головную боль старух.
Ух, опасен пуха дух!

Если соблюдать стихотворный размер, можно довольно быстро запомнить:

Три, четырнадцать, пятнадцать, девять два, шесть пять, три пять
Восемь девять, семь и девять, три два, три восемь, сорок шесть
Два шесть четыре, три три восемь, три два семь девять, пять ноль два
Восемь восемь и четыре, девятнадцать, семь, один

Как ещё нередко называют число Пи. Кто открыл число Пи? История вычислений

Уже много веков и даже, как ни странно, тысячелетий люди понимают важность и ценность для науки математической постоянной, равной отношению длины окружности к ее же диаметру.  число Пи, до сих пор неизвестно, но к нему имели отношение самые лучшие математики на протяжении всей нашей истории. Большинство из них хотели выразить его рациональным числом

Интересные сведения о числе Пи

1. Исследователи и истинные поклонники числа Пи организовали клуб, для вступления в который требуется знать наизусть достаточно большое количество его знаков.

2. С 1988 года празднуется «День числа Пи», который приходится на 14 марта. Готовят салаты, торты, печенья, пирожные с его изображением.

3. Число Пи уже переложили на музыку, при этом оно весьма неплохо звучит. Ему даже воздвигли памятник в американском Сиэтле перед зданием городского Музея искусств.

Древний период

В то далекое время число Пи старались вычислить при помощи геометрии. То, что это число постоянно для самых разных окружностей, знали еще геометры в Древнем Египте, Вавилоне, Индии и Древней Греции, утверждавшие в своих работах, что оно всего лишь немного больше трех.

В одной из священных книг джайнизма (древняя индийская религия, которая возникла в VI в. до н. э.) упоминается, что тогда число Пи считалось равным корню квадратному из десяти, что в итоге дает 3,162… .

Древнегреческие математики проводили измерение окружности методом построения отрезка, а вот для того, чтобы измерить круг, им приходилось строить равновеликий квадрат, то есть фигуру, равную ему по площади.

Когда еще не знали десятичных дробей, великий Архимед нашел значение числа Пи с точностью 99,9%. Он открыл способ, который стал основой многих последующих вычислений, вписывал в окружность и описывал вокруг нее правильные многоугольники. В результате Архимед рассчитал значение числа Пи как отношение 22 / 7 ≈ 3,142857142857143.

В Китае, математик и придворный астроном, Цзу Чунчжи в V веке до н. э. обозначил более точное значение числа Пи, рассчитав его до семи цифр после запятой и определил его значение между числами 3, 1415926 и 3,1415927. Более 900 лет понадобилось ученым, чтобы продолжить дальше этот цифровой ряд.

Средние века

Известный индийский ученый Мадхава, который жил на рубеже XIV — XV веков, ставший основателем Керальской школы астрономии и математики, впервые в истории стал работать над разложением тригонометрических функций в ряды. Правда, сохранились всего лишь два его труда, а на другие известны лишь ссылки и цитаты его учеников. В научном трактате «Махаджьянаяна», который приписывают Мадхаве, указано, что число Пи равно 3,14159265359. А в трактате «Садратнамала» приведено число с еще большим количеством точных знаков после запятой: 3,14159265358979324. В указанных числах последние цифры не соответствуют правильному значению.

В XV веке самаркандский математик и астроном Ал-Каши вычислил число Пи с шестнадцатью знаками после запятой. Его результат считался наиболее точным в течение последующих 250 лет.

У. Джонсон, математик из Англии, одним из первых смог обозначить отношение длины окружности к ее диаметру буквой π. Пи — это первая буква греческого слова «περιφέρεια» — окружность. Но этому обозначению удалось стать общепринятым лишь после того, как им воспользовался в 1736 году более известный ученый Л. Эйлер.

Заключение

Современные ученые продолжают работать над дальнейшими вычислениями значений числа Пи. Для этого уже используют суперкомпьютеры. В 2011 г. ученый из Сигэру Кондо, сотрудничая с американским студентом Александром Йи, произвели правильный расчет последовательности из 10 триллионов цифр. Но до сих пор так и неясно, кто открыл число Пи, кто впервые задумался над этой проблемой и произвел первые расчеты этого, по-настоящему мистического числа.

Тайны числа Пи

В романе Карла Сагана «Контакт», по которому снят одноименный фильм, инопланетяне сообщают героине, что среди знаков Пи содержится тайное послание от Бога. С некоторой позиции цифры в числе перестают быть случайными и представляют себе код, в котором записаны все секреты Мироздания.

Этот роман на самом деле отразил загадку, занимающую умы математиков всей планеты: является ли число Пи нормальным числом, в котором цифры разбросаны с одинаковой частотой, или с этим числом что-то не так. И хотя ученые склоняются к первому варианту (но не могут доказать), число Пи выглядит очень загадочно. Один японец как то подсчитал, сколько раз встречаются числа от 0 до 9 в первом триллионе знаков Пи. И увидел, что числа 2, 4 и 8 встречаются чаще, чем остальные. Это может быть одним из намеков на то, что Пи не совсем нормальное, и цифры в нем действительно не случайны.

Вспомним всё, что мы прочли выше, и спросим себя, какое еще иррациональное и трансцендентное число так часто встречается в реальном мире?

А в запасе имеются еще странности. Например, сумма первых двадцати цифр Пи равна 20, а сумма первых 144 цифр равна «числу зверя» 666.

Главный герой американского сериала «Подозреваемый» профессор Финч рассказывал студентам, что в силу бесконечности числа Пи в нем могут встретиться любые комбинации цифр, начиная от цифр даты вашего рождения до более сложных чисел. Например, на 762-ой позиции находится последовательность из шести девяток. Эта позиция называется точкой Фейнмана в честь известного физика, который заметил это интересное сочетание.

Нам известно также, что число Пи содержит последовательность 0123456789, но находится она на 17 387 594 880-й цифре.

Все это означает, что в бесконечности числа Пи можно обнаружить не только интересные сочетания цифр, но и закодированный текст «Войны и Мира», Библии и даже Главную Тайну Мироздания, если таковая существует.

Кстати, о Библии. Известный популяризатор математики Мартин Гарднер в 1966 году заявил, что миллионным знаком числа Пи (на тот момент еще неизвестным) будет число 5. Свои расчеты он объяснил тем, что в англоязычной версии Библии, в 3-й книге, 14-й главе, 16-м стихе (3-14-16) седьмое слово содержит пять букв. Миллионную цифру получили спустя восемь лет. Это было число пять.

Стоит ли после этого утверждать, что число Пи случайно?

Примечания

1. Это определение пригодно только для евклидовой геометрии. других геометриях отношение длины окружности к длине её диаметра может быть произвольным. Например, в геометрии Лобачевского это отношение меньше, чем
2. Lambert, Johann Heinrich. Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques, стр. 265–322.
3. Доказательство Клейна приложено к работе «Вопросы элементарной и высшей математики», ч. 1, вышедшей в Гёттингене в 1908 году.
4. Weisstein, Eric W. Постоянная Гельфонда (англ.) на сайте Wolfram MathWorld.
5. 1
   2
   Weisstein, Eric W. Иррациональное число (англ.) на сайте Wolfram MathWorld.
6. Модулярные функции и вопросы трансцендентности
7. Weisstein, Eric W. Pi Squared (англ.) на сайте Wolfram MathWorld.
8. наши дни с помощью ЭВМ число вычислено с точностью до миллиона знаков, что представляет скорее технический, чем научный интерес, потому что такая точность в общем-то никому не нужна.
   Точность вычисления ограничивается обычно наличными ресурсами компьютера, — чаще всего временем, несколько реже — объёмом памяти.
9. Brent, Richard (1975), Traub, J F, ed., ««Multiple-precision zero-finding methods and the complexity of elementary function evaluation»», Analytic Computational Complexity (New York: Academic Press): 151–176, (англ.)
10. Jonathan M Borwein. Pi: A Source Book. — Springer, 2004. — ISBN 0387205713. (англ.)
11. 1
    2
    David H. Bailey, Peter B. Borwein, Simon Plouffe. On the Rapid Computation of Various Polylogarithmic Constants // Mathematics of Computation. — 1997. — Т. 66, вып. 218. — С. 903-913. (англ.)
12. Fabrice Bellard. A new formula to compute the nth binary digit of pi (англ.). Проверено 11 января 2010. Архивировано из первоисточника 22 августа 2011.
13. Simon Plouffe. Indentities inspired by Ramanujan’s Notebooks (part 2) (англ.). Проверено 11 января 2010. Архивировано из первоисточника 22 августа 2011.
14. Установлен новый рекорд точности вычисления числа π
15. Pi Computation Record
16. Число «Пи» рассчитано с рекордной точностью
17. 1
    2
    5 Trillion Digits of Pi — New World Record (англ.)
18. Определено 10 триллионов цифр десятичного разложения для π
19. 1
    2
    Round 2… 10 Trillion Digits of Pi
20. Weisstein, Eric W. Мера иррациональности (англ.) на сайте Wolfram MathWorld.
21. Weisstein, Eric W. Pi (англ.) на сайте Wolfram MathWorld.
22. en:Irrational number#Open questions
23. Some unsolved problems in number theory
24. Weisstein, Eric W. Трансцендентное число (англ.) на сайте Wolfram MathWorld.
25. An introduction to irrationality and transcendence methods
26. Обман или заблуждение? Квант № 5 1983 год
27. Г. А. Гальперин. Биллиардная динамическая система для числа пи.
28. Лудольфово число. Пи. Pi.
29. Chinese student breaks Guiness record by reciting 67,890 digits of pi
30. Interview with Mr. Chao Lu
31. How can anyone remember 100,000 numbers? — The Japan Times, 17.12.2006.
32. Pi World Ranking List
33. The Indiana Pi Bill, 1897 (англ.)
34. В. И. Арнольд любит приводить этот факт, см. например книгу Что такое математика (ps), стр. 9.
35. Alexander J. Yee. y-cruncher — A Multi-Threaded Pi-Program. y-cruncher.
36. Статья в Los Angeles Times «Желаете кусочек »? (название обыгрывает сходство в написании числа и слова pie (англ. пирог)) (недоступная ссылка с 22-05-2013 (859 дней) — история, копия) (англ.).

***

Что общего между колесом от Лады Приоры, обручальным кольцом и блюдцем вашего кота? Вы, конечно, скажете красота и стиль, но я осмелюсь с вами поспорить. Число Пи!
Это число, объединяющее все окружности, круги и округлости, к коим в частности можно отнести и мамино кольцо, и колесо от любимой папиной машины и даже блюдце любимого кота Мурзика. Готов поспорить, что в рейтинге самых популярных физических и математических констант число Пи несомненно займет первую строчку. Но что скрывается за ним? Может какие-то страшные ругательства математиков? Давайте попробуем разобраться в этом вопросе.

Квадраты отдыхают, восьмиугольники правят миром

Мы оценили число π как 3,4, но, честно говоря, мы бы добились большего с линейкой и нитью. Что же делает нашу оценку настолько плохой?

Квадраты неэффективны. Они не очень хорошо аппроксимируют круг, а в ошибках нашего вычисления виноваты зазоры между ними. Однако увеличение числа сторон (например, до восьмиугольника) даст нам более точную подгонку и, таким образом, более верное значение числа π.

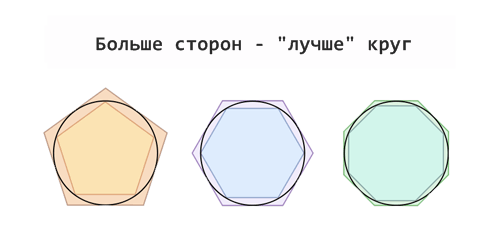
Отлично! По мере увеличения количества сторон многоугольником мы всё больше приближаемся к форме круга.

Итак, как нам теперь найти периметр восьмиугольника? Калид говорит: «Я не уверен, что я помню формулу для нахождения его периметра». Конечно, можно использовать 16-угольники или 32-угольники для улучшения нашей оценки длины окружности. Однако вопрос тот же: чему равны их периметры?

О да, вот они, те самые трудные вопросы. К счастью, Архимед использовал своего рода креативный подход к тригонометрии, в рамках которого он приближал круг двумя многоугольниками с числом сторон 2n (например, 23 = 8, 24 = 16 и т.д.), одним внешним и одним внутренним. На каждом шаге производится оценка длины окружности, которая находится между периметром внешнего и периметром внутреннего многоугольника. Если p_n — это периметр внутреннего многоугольника с числом сторон 2n, а P_n — периметр внешнего многоугольника с числом сторон 2n, между которыми заключён наш круг, длина окружности которого l, то p_n ≤ l ≤ P_n. На каждом шаге увеличивается число сторон многоугольников (8, 16, 32 и т.д.), и таким образом достигается всё более точная оценка.

Таким образом, Архимед проводил приближенную оценку длин различных окружностей и уже на их основе установил величину числа π. Мы же, зная, что длина окружности равна πd, где d — диаметр окружности, и взяв окружность единичного диаметра, можем тем же самым способом оценить число π.

Периметр внутреннего многоугольника. Одна сторона внутреннего многоугольника a (например, квадрата) равна sin(x/2), где x — это угол, дополняющий угол нашего многоугольника до π.

Это легко понять на примере квадрата. Из центра круга (который совпадает с центром квадрата) проведём два радиуса в вершины нашего многоугольника (квадрата в данном случае). Это будут радиусы, так как вершины вписанного многоугольника лежат на окружности. Эти радиусы являются биссектрисами соответствующих углов многоугольника, т.е., делят угол пополам. Таким образом, в получившемся треугольнике угол, прилегающий к основанию (величину которого мы и хотим найти), равен (π—x)/2.

Из вершины треугольника опустим перпендикуляр к основанию. Получится прямоугольный треугольник, у которого один из катетов равен a/2, а гипотенуза равна радиусу нашей окружности, и, как следствие, ½ (так как диаметр окружности 1).

В случае квадрата, например, получится, что одна сторона внутреннего квадрата равна sin (90/2) = sin (45) ~ 0,7. Затем измеряем полный периметр: 4 * 0,7 = 2,8. Получаем тот же результат, что у нас был. Аналогичные вычисления можно провести и для вписанного восьмиугольника с учётом того, что угол там равен 45.

Периметр внешнего многоугольника. Точно таким же образом узнаём, что один наружный сегмент равен tg(х/2), где х представляет собой угол между сторонами. Таким образом, одна часть внешнего периметра tg(45) = 1, а общий периметр = 4.

Изящно — у нас есть простая формула! Добавление большего количества сторон делает угол меньше:

• Квадраты имеют внутренний периметр 4 * sin(90/2).
• Восьмиугольники имеют восемь углов по 45 градусов с внутренним периметром 8 * sin(45/2).

Попробуйте это! С квадратом (4 стороны) мы имеем 91% точности, а с восьмиугольником (8 сторон) мы достигаем 98%!

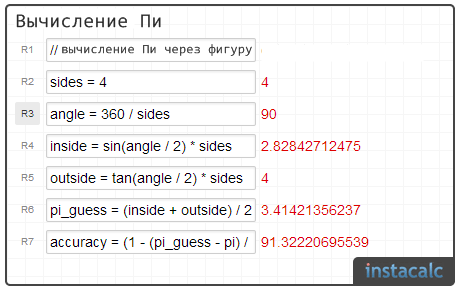
Но есть одна проблема: у Архимеда не было калькулятора с волшебной кнопкой «sin». Вместо этого он использовал тождества, чтобы выразить sin и tan, а также связать между собой периметры вписанных и описанных вокруг нашей окружности многоугольников с числом сторон 2n и 2n+1.

Для этого нужно сделать следующее. Так как мы используем 2n—многоугольники, то при переходе к каждому следующему соответствующий угол у многоугольника уменьшается вдвое.

Если для n стороны соответственно внутреннего и внешнего многоугольников равны s_n=sin(x/2), T_n=tg(x/2), то для n+1 будет s_n+1=sin(x/4), T_n+1=tg(x/4).

Выразим формулы для (n+1) через формулы для n.

Если перейти к периметрам (помня, что у нас 2n-угольники), то получим:

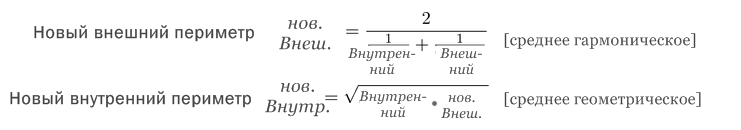
Эти формулы используют только арифметику, тригонометрия здесь не требуется. Так как мы начали с такими известными числами как √2 и √1, мы можем повторно применить эту формулу, чтобы увеличить количество сторон и ещё ближе подойти к значению π.

По стопам Архимеда

— Какое из двух числе больше 22/7 или 3.14 ? — Они равны. — Почему ? — Каждое из них равно π . А. А. Власов. Из Экзаменационного билета.

Некоторы полагают, что дробь 22/7 и чисо π тождественно равны. Но это является заблуждением. Помимо вышеприведенного неверного ответа на экзамене (см. эпиграф) к этой группе можно также добавить одну весьма занимательную головоломку. Задание гласит: «переложите одну спичку так, чтобы равенство стало верным».

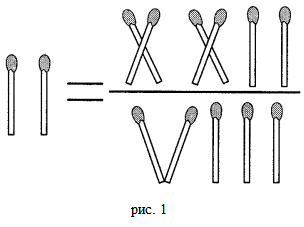
Решение будет таковым: нужно образовать «крышу» для двух вертикальных спичек слева, используя одну из вертикальных спичек в знаменателе справа. Получится визуальное изображение буквы π .

Многие знают, что приближение π = 22/7 определил древнегреческий математик Архимед. В честь этого часто такое приближение называют «Архимедовым» числом. Архимеду удалось не только установить приближенное значение для π, но также найти точность этого приближения, а именно – найти узкий числовой промежуток, которому принадлежит значение π . В одной из своих работ Архимед доказывает цепь неравенств, которая на современный лад выглядела бы так:

10	6336	14688	1
3	π
71	1	1	7
2017	4673
4	2

можно записать проще: 3,140 909 π π за 3,14 для удобства подсчета.

Пожалуй, самая известная формула среди школьников, в которой используется π , это – формула длины и площади окружности. Первая – формула площади круга – записывается так:

π D 2

S= π R 2 =

4

где S – площадь окружности, R – ее радиус, D – диаметр окружности.

Длина окружности, или, как ее иногда называют, периметр окружности, вычисляют по формуле:

где C – длина окружности, R – радиус, d – диаметр окружности.

Понятно, что диаметр d равен двум радиусам R.

Из формулы длины окружности можно легко найти радиус окружности:

C	C
R=	=
2 π	d

Обозначения для этих формул остаются те же.

Диаметр окружности можно найти по формуле:

C
D=	=2R
π

где D – диаметр, С – длина окружности, R – радиус окружности.

Это базовые формулы, знать которые должен каждый ученик. Также иногда приходится вычислять площадь не всей окружности, а только ее части – сектора. Поэтому представляем вам её – формулу для вычисления площади сектора окружности. Выглядит она так:

α
S	=	π R 2
360˚

где S – площадь сектора, R – радиус окружности, α – центральный угол в градусах.

Тайны числа Пи

В романе Карла Сагана «Контакт», по которому снят одноименный фильм, инопланетяне сообщают героине, что среди знаков Пи содержится тайное послание от Бога. С некоторой позиции цифры в числе перестают быть случайными и представляют себе код, в котором записаны все секреты Мироздания.

Этот роман на самом деле отразил загадку, занимающую умы математиков всей планеты: является ли число Пи нормальным числом, в котором цифры разбросаны с одинаковой частотой, или с этим числом что-то не так. И хотя ученые склоняются к первому варианту (но не могут доказать), число Пи выглядит очень загадочно. Один японец как то подсчитал, сколько раз встречаются числа от 0 до 9 в первом триллионе знаков Пи. И увидел, что числа 2, 4 и 8 встречаются чаще, чем остальные. Это может быть одним из намеков на то, что Пи не совсем нормальное, и цифры в нем действительно не случайны.

Вспомним всё, что мы прочли выше, и спросим себя, какое еще иррациональное и трансцендентное число так часто встречается в реальном мире?

А в запасе имеются еще странности. Например, сумма первых двадцати цифр Пи равна 20, а сумма первых 144 цифр равна «числу зверя» 666.

Главный герой американского сериала «Подозреваемый» профессор Финч рассказывал студентам, что в силу бесконечности числа Пи в нем могут встретиться любые комбинации цифр, начиная от цифр даты вашего рождения до более сложных чисел. Например, на 762-ой позиции находится последовательность из шести девяток. Эта позиция называется точкой Фейнмана в честь известного физика, который заметил это интересное сочетание.

Нам известно также, что число Пи содержит последовательность 0123456789, но находится она на 17 387 594 880-й цифре.

Все это означает, что в бесконечности числа Пи можно обнаружить не только интересные сочетания цифр, но и закодированный текст «Войны и Мира», Библии и даже Главную Тайну Мироздания, если таковая существует.

Кстати, о Библии. Известный популяризатор математики Мартин Гарднер в 1966 году заявил, что миллионным знаком числа Пи (на тот момент еще неизвестным) будет число 5. Свои расчеты он объяснил тем, что в англоязычной версии Библии, в 3-й книге, 14-й главе, 16-м стихе (3-14-16) седьмое слово содержит пять букв. Миллионную цифру получили спустя восемь лет. Это было число пять.

Стоит ли после этого утверждать, что число Пи случайно?

Увлеченные математикой люди по всему миру ежегодно съедают по кусочку пирога четырнадцатого марта — ведь это день числа Пи, самого известного иррационального числа. Эта дата напрямую связана с числом, первые цифры которого 3,14. Пи — это соотношение длины окружности к диаметру. Так как оно иррациональное, записать его в виде дроби невозможно. Это бесконечно длинное число. Его обнаружили тысячи лет назад и с тех пор постоянно изучают, но остались ли у Пи какие-нибудь секреты? От древнего происхождения до неопределенного будущего вот несколько наиболее интересных фактов о числе Пи.

Константа и общество

Некоторые особенностей числа:

1. Константа является иррациональной величиной. Это значит, что её невозможно представить в виде отношения двух чисел. Кроме того, в его записи отсутствует какая-либо закономерность.
2. Повторяющиеся подряд знаки в константе – не редкость. Так, на каждые 20-30 символов обычно встречается хотя бы 2 идущих подряд цифры. Последовательности из 3 знаков уже более редкие, они попадаются с частотой около 1 повторения на 150-300 символов. А на 763 знаке начинается цепочка из 6 идущих подряд девяток. Это место в записи даже имеет собственное имя – точка Фейнмана.
3. Если рассматривать первый миллион символов, то по статистике самыми редкими цифрами в нём окажутся 6 и 1, а самыми частыми – 5 и 4.
4. Цифра 0 появляется в последовательности позже остальных, лишь на 31 знаке.
5. В тригонометрии угол в 360 градусов и константа тесно связаны. Как ни странно, но на 358, 359 и 360 позиции после запятой расположено число 360.

С целью обмена информацией об открытиях был учреждён Пи-клуб. Желающим вступить в него приходится выдерживать нелёгкий экзамен: будущий член математического сообщества должен верно назвать на память как можно больше знаков постоянной.

Конечно, заучивание длинной числовой последовательности, не имеющей закономерностей и повторений — занятие достаточно трудное. Чтобы облегчить задачу, придумываются различные тексты и стихотворения, в которых количество букв в слове соответствует определённой цифре константы. Этот способ запоминания популярен у членов Пи-клуба. Один из самых длинных рассказов содержал 3834 первых знаков числа.

Памятник у Музея искусств в Сиэтле

Однако признанные рекордсмены по заучиванию – это, конечно же, жители Китая и Японии. Так, японец Акира Харагути смог выучить свыше 83 тысяч цифр после запятой. А китаец Лю Чао прославился как человек, который смог назвать 67890 символов числа Пи за рекордное время – 24 часа. При этом средняя скорость составила 47 знаков за 1 минуту. Изначально его цель была назвать 93 тысячи цифр, однако им была допущена ошибка, после которой он не стал продолжать.

Чтобы подчеркнуть значение константы, в Сиэтле перед Музеем искусств был воздвигнут памятник в виде огромной греческой буквы π.

Кроме того, с 1988 года каждое 14 марта отмечается день числа Пи. Дата совпадает с первыми знаками постоянной – 3,14. Празднуют его после 1:59. В этот день заинтересованные люди угощаются тортами и печеньем с символом Пи, после чего проводят различные математические конкурсы и викторины. Кстати, именно в этот день родились А.Эйнштейн, астроном Скиапарелли и космонавт Сернан.

Число Пи – удивительная константа, которая нашла своё применения в самых разных областях, начиная от техники и строительства и заканчивая сферами искусства

Как и любая другая величина, которая применяется часто и которую невозможно вычислить полностью, она всегда будет привлекать к себе внимание математиков, физиков и других учёных

Чему равно число Пи
мы знаем и помним со школы. Оно равно 3.1415926 и так далее… Обычному человеку достаточно знать, что это число получается, если разделить длину окружности на ее диаметр. Но многим известно, что число Пи возникает в неожиданных областях не только математики и геометрии, но и в физике. Ну а если вникнуть в подробности природы этого числа, то можно заметить много удивительного среди бесконечного ряда цифр. Возможно ли, что Пи скрывает самые сокровенные тайны Вселенной?

Свойства[править | править код]

Соотношенияправить | править код

Известно много формул с числом π\pi:

Франсуа Виет, 1593:

2π=12⋅12+1212⋅12+1212+1212⋅…\frac{2}{\pi}=\sqrt{\frac{1}{2}} \cdot \sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}}} \cdot \sqrt{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{1}{2}+\frac{1}{2} \sqrt{\frac{1}{2}}}} \, \cdot \ldots

Формула Валлиса:

21⋅23⋅43⋅45⋅65⋅67⋅87⋅89⋯=π2\frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots = \frac{\pi}{2}

Формула Валлиса-Александрова:

21⋅23⋅43⋅45⋅65⋅67⋅87⋅(89⋅14+1)+34⋯=π2 \frac{2}{1}\cdot \frac{2}{3}\cdot \frac{4}{3}\cdot \frac{4}{5}\cdot \frac{6}{5}\cdot \frac{6}{7}\cdot \left \cdots = \frac{\pi}{2}

Модифицированная формула Валлиса:

limm→∞(m!)424m(2m)!2m=π\lim \limits_{m\rightarrow \infty }{\frac { (m!)^{4}{2}^{4m}}{\left ^{2}m}} = \pi

Произведения:

π=3⋅32∏k=1∞k2k2−(13)2\pi=3\cdot \frac{\sqrt{3}}{2} \prod \limits_{k=1}^{\infty}\frac{k^2}{k^2-\left (\frac{1}{3}\right )^2}π=32⋅32∏k=1∞k2k2−(23)2\pi=\frac{3}{2}\cdot \frac{\sqrt{3}}{2} \prod \limits_{k=1}^{\infty}\frac{k^2}{k^2-\left (\frac{2}{3}\right )^2}π=4⋅22∏k=1∞k2k2−(14)2\pi=4\cdot \frac{\sqrt{2}}{2} \prod \limits_{k=1}^{\infty}\frac{k^2}{k^2-\left (\frac{1}{4}\right )^2}π=43⋅22∏k=1∞k2k2−(34)2\pi=\frac{4}{3}\cdot \frac{\sqrt{2}}{2} \prod \limits_{k=1}^{\infty}\frac{k^2}{k^2-\left (\frac{3}{4}\right )^2}π=6⋅12∏k=1∞k2k2−(16)2\pi=6\cdot \frac{1}{2} \prod \limits_{k=1}^{\infty}\frac{k^2}{k^2-\left (\frac{1}{6}\right )^2}π=65⋅12∏k=1∞k2k2−(56)2\pi=\frac{6}{5}\cdot \frac{1}{2} \prod \limits_{k=1}^{\infty}\frac{k^2}{k^2-\left (\frac{5}{6}\right )^2}π=4⋅∏k=1∞k2+kk2+k+14\pi=4\cdot\prod \limits_{k=1}^{\infty}\frac{k^2+k}{k^2+k+\frac{1}{4}}π=92⋅32∏k=1∞k2+kk2+k+29\pi=\frac{9}{2}\cdot\frac{\sqrt{3}}{2}\prod \limits_{k=1}^{\infty} \frac{k^2+k}{k^2+k+ \frac{2}{9}}π=163⋅22∏k=1∞k2+kk2+k+316\pi=\frac{16}{3}\cdot\frac{\sqrt{2}}{2}\prod \limits_{k=1}^{\infty} \frac{k^2+k}{k^2+k+ \frac{3}{16}}π=365⋅12∏k=1∞k2+kk2+k+536\pi=\frac{36}{5}\cdot\frac{1}{2}\prod \limits_{k=1}^{\infty} \frac{k^2+k}{k^2+k+ \frac{5}{36}}π=23∏k=1∞(2k−1)12−k(2k+3)k+122k+1(kk+1)2k\pi= 2\sqrt{3}\prod \limits_{k=1}^{\infty}\frac{\left ( 2k-1 \right )^{\frac 12 -k} \left ( 2k+3 \right )^{k+\frac 12}}{2k+1}\left (\frac{k}{k+1} \right )^{2k}

Ряд Лейбница:

11−13+15−17+19−⋯=π4\frac{1}{1} — \frac{1}{3} + \frac{1}{5} — \frac{1}{7} + \frac{1}{9} — \cdots = \frac{\pi}{4}

Тождество Эйлера:

eiπ+1=e^{i \pi} + 1 = 0\;

Т. н. «интеграл Пуассона» или «интеграл Гаусса»

∫−∞+∞ e−x2dx=π\int\limits_{-\infty}^{+\infty}\ e^{-x^2}{dx} = \sqrt{\pi}

Интегральный синус

∫−∞+∞sin Синус (x)xdx=π\int\limits_{-\infty }^{+\infty }{\frac{\sin(x)}{x}dx}=\pi

Интегральный косинус

∫−∞+∞1−cos Косинус (x)x2dx=π\int\limits_{-\infty }^{+\infty }{\frac{1-\cos(x)}{x^2}dx}=\pi

Интегральный тангенс

∫−∞+∞tg(x)xdx=π\int\limits_{-\infty }^{+\infty }{\frac{tg(x)}{x}dx}=\pi

Интегральный котангенс

∫−∞+∞1−x⋅ctg(x)x2dx=π\int\limits_{-\infty }^{+\infty }{\frac{1-x \cdot ctg(x)}{x^2}dx}=\pi

Интегральный арктангенс

2∫−∞∞x−arctg(x)x3dx=π2 \int \limits _{-\infty }^{\infty }\! \frac {x-arctg(x)}{x^3}{dx}=\pi

Трансцендентность и иррациональностьправить | править код

• Иррациональность числа π\pi была впервые доказана Иоганном Ламбертом в 1767 году путём разложения числа e−12n\frac{e-1}{2^n} в непрерывную дробь. В 1794 году Лежандр привёл более строгое доказательство иррациональности чисел π\pi и π2\pi^2.
• В 1882 годe профессору Кёнигсбергского, а позже Мюнхенского университета Фердинанду Линдеману удалось доказать трансцендентность числа π\pi. Доказательство упростил Феликс Клейн в 1894 году

  Поскольку в геометрии Евклида площадь круга и длина окружности являются функциями числа π\pi, то доказательство трансцендентности π\pi положило конец спору о квадратуре круга, длившемуся более 2,5 тысяч лет.

Нормальное ли число Пи?

Число Пи определенно странное, но насколько оно подчиняется нормальным математическим законам? Ученые уже разрешили многие вопросы, связанные с этим иррациональным числом, но некоторые загадки остаются. К примеру, неизвестно, насколько часто используются все цифры — цифры от 0 до 9 должны использоваться в равной пропорции. Впрочем, по первым триллионам цифр статистика прослеживается, но из-за того, что число бесконечное, доказать точно ничего невозможно. Есть и другие проблемы, которые пока ускользают от ученых. Вполне возможно, что дальнейшее развитие науки поможет пролить на них свет, но на данный момент это остается за пределами человеческого интеллекта.